Quantum Leap: Revolutionizing the Process of Solving Complex Problems

Quantum computers, which use diverse qubits, are now leading the way in addressing intricate optimization issues such as the traveling salesman dilemma, which have historically been characterized by computing inefficiency. Researchers have demonstrated via meticulous mathematical analysis that quantum computing has the potential to completely revolutionize problem-solving. This is achieved by providing a more efficient polynomial increase in calculation time when compared to traditional approaches, resulting in improved answers.

The issue of the traveling salesman is often regarded as a prominent illustration of a combinatorial optimization problem. A team based in Berlin, under the leadership of Prof. Dr. Jens Eisert, a theoretical physicist affiliated with Freie Universität Berlin and HZB, has shown that quantum computers may effectively and expeditiously tackle a specific category of these issues, surpassing the performance of traditional approaches.

Quantum computers use qubits, which deviate from the binary nature of traditional logic circuits by allowing them to assume any value within the range of zero to one. The realization of these qubits involves the use of very chilled atoms, ions, or superconducting circuits. However, the construction of a quantum computer with a large number of qubits remains a physically intricate task. Nevertheless, mathematical techniques may already be used to investigate the potential accomplishments of fault-tolerant quantum computers in the future.

There are numerous misconceptions about it, occasionally along with exaggerated claims and exaggerated enthusiasm. However, we have adopted a rigorous approach to the problem, using mathematical methodologies, and have achieved substantial outcomes in relation to the subject matter. According to Prof. Dr. Jens Eisert, the leader of a collaborative research group at Freie Universität Berlin and Helmholtz-Zentrum Berlin, our primary objective is to elucidate the specific contexts in which any potential benefits may exist.

Taking on Hard Problems
One well-known example is the situation of the moving salesman: A tourist needs to see a few places and then go back to his home town. What is the fastest way to get there? This problem is simple to understand at first, but it gets harder as the number of places grows and the time it takes to solve it rises.

The traveling salesman problem is a very important optimization problem in the business world. These problems can be about train networks, transportation, or making the best use of resources. Approximation methods can be used to find answers that are good enough.

Exploring Quantum Solutions and Advancements
The team, under the direction of Jens Eisert and his colleague Jean-Pierre Seifert, has used only analytical techniques to evaluate a quantum computer’s capacity for solving this particular set of issues. Engage in a timeless thought experiment utilizing the tools of a physicist and a wealth of knowledge.

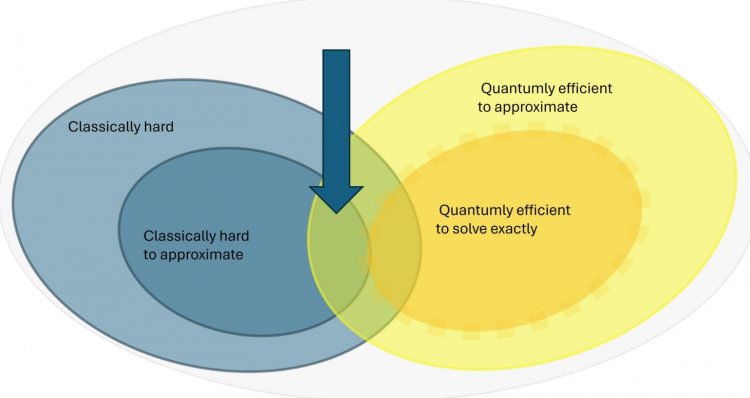
“We make the assumption, regardless of how it is physically implemented, that there are sufficient qubits and analyze the potential for conducting computational operations with them,” clarifies Vincent Ulitzsch, a PhD student at the Technical University of Berlin. Through their analysis, they discovered striking parallels to a widely recognized issue in cryptography: the encryption of data. “We discovered that a subclass of these optimization problems could be solved using the Shor algorithm,” explains Ulitzsch.

With this approach, the computing time no longer grows exponentially with the number of cities but instead increases at a polynomial rate, specifically Nx, where x is a constant. The solution obtained in this manner is also significantly superior in quality compared to the approximate solution obtained using the conventional algorithm.

“We have demonstrated that quantum computers possess a fundamental edge over classical computers in certain instances of a specific yet highly significant and practically applicable category of combinatorial optimization problems,” explains Eisert.